정보 검색(Information Retrieval) 평가는 어떻게 하는 것이 좋을까?(2/2)
지난 글에서는 IR의 평가 기준이 될 수 있는 정확도(accuracy), 정밀도(precision), 재현율(recall)에 대해 살펴보았다. 정확도, 정밀도, 재현율은 전반적인 IR 성능을 평가할 수 있지만, 우선순위(rank)에 대한 정확성을 판단할 수 없다. 인기 시스템(recommender system)이나 인기순 검색 같은 경우 관련된 컨텐츠가 얼마나 상위에 노출되어있는가가 중요하기 때문에 우선순위에 대한 중요도를 평가하는 것이 필요하다.
이번 글에서는 우선순위를 고려한 평가 모델인 MRR(Mean Reciprocal Rank), MAP(Mean Average Precision), NDCG(Normalized Discounted Cumulative Gain)에 대해서 알아보고자 한다.
MRR
MRR(Mean Reciprocal Rank)은 우선순위를 고려한 평가기준 중 가장 간단한 모델이다. 아래의 알고리즘을 살펴보자.

위 알고리즘을 해석하면 아래와 같다.
- 각 사용자마다 제공한 추천 컨텐츠 중 관련있는 컨텐츠 중 가장 높은 위치를 역수로 계산(1/k)한다.
- 사용자마다 계산된 점수를 모아 평균을 계산한다.
실제 예를 통해 이해하기 위해 아래 그림을 살펴보자.
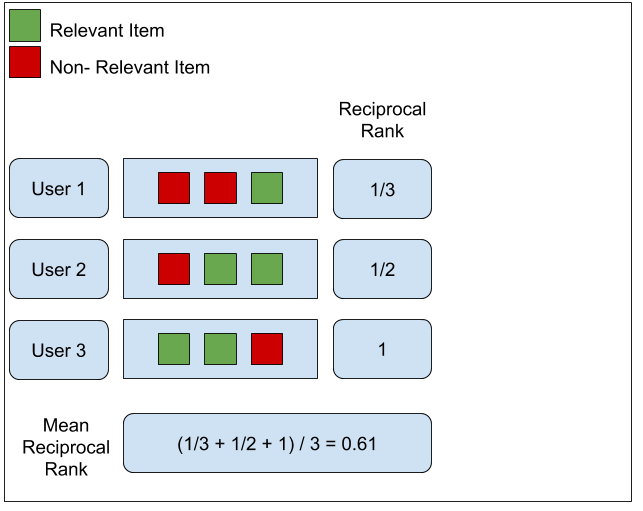
이 그림에서 보듯이 3명의 사용자에 각기 다른 추천 컨텐츠 목록을 제공하였다. 각 컨텐츠는 관련이 있는 컨텐츠와 관련이 없는 컨텐츠로 구분되는데 각각 녹색과 붉은색으로 구분한다. 사용자 1은 가장 상위의 관련된 컨텐츠가 3번째이기 때문에 reciprocal rank가 1/3이 된다. 사용자 2는 2번째 컨텐츠가 가장 높은 순위의 관련 컨텐츠이므로 reciprocal rank가 1/2이 된다. 마지막으로 사용자 3은 첫 번째 컨텐츠가 가장 높은 순위의 관련 컨텐츠이므로 reciprocal rank가 1/1 = 1이 된다. 이렇게 구해진 모든 사용자 reciprocal rank의 평균값을 계산하면 (1/3 + 1/2 + 1) / 3 = 0.61이라는 결과를 얻을 수 있고 이는 해당 IR의 MRR 값이 된다.
이와 같이 MRR은 사용자가 몇 개의 컨텐츠에 관심이 있었는지, 각 관련 컨텐츠는 어느 위치에 있었는지를 고려하지 않는다. 오직, 가장 상위의 관련 컨텐츠의 위치만을 고려하여 점수를 계산함으로써 가장 관련있는 컨텐츠가 얼마나 상위에 올라가 있는지를 평가한다.
MRR의 장점
- 간단하고 쉽다.
- 제공된 목록 중 가장 상위의 관련된 컨텐츠에만 집중하기 때문에, 사용자에 가장 관련있는 컨텐츠가 최상위에 있는가를 평가할 때 용이하다.
- 새로운 컨텐츠가 아니라 이미 사용자가 알고 있는 컨텐츠 중 가장 선호할만한 컨텐츠를 보여주고자 할 때 좋은 평가 기준이 된다.
MRR의 단점
- 제공된 목록 중 하나의 컨텐츠에만 집중하기 때문에 나머지 부분에 대해서는 평가하지 않는다.(2, 3번째 관련 컨텐츠에 대해서는 평가를 하지 않는다.)
- 관련 컨텐츠의 개수가 달라도 첫 번째 관련 컨텐츠의 위치가 같은 경우 같은 점수를 가지므로 변별력을 가지기 어렵다.
- 사용자가 컨텐츠에 대해 잘 알지 못해 여러 번 탐색을 해야 하는 경우 살펴봐야 하는(관련있는) 컨텐츠의 개수가 1개 이상일 가능성이 높으므로 좋은 평가 기준이 되기 어렵다.
MRR은 장단점이 뚜렷한 평가 모델로써, 사용자가 원하는 목적이 비교적 뚜렷하고 잘 알고 있는 알려진 컨텐츠를 추천하는 IR(배달 어플리케이션의 배달 음식점 검색)을 평가할 때 좋은 모델이 될 수 있다.
MAP
앞서 MRR은 간단하고 쉽게 평가를 할 수 있으나 관련된 컨텐츠 중 가장 상위의 컨텐츠의 위치를 평가의 기준으로 삼기 때문에 관련된 컨텐츠 모두를 평가하기 어렵다는 단점이 있었다. 이러한 단점을 해결하기 위해 가장 쉽게 생각할 수 있는 방법은 상위 N개까지의 정밀도를 구하는 것(Precision@N)이다. 이 방법은 관련된 컨텐츠의 개수를 점수에 반영할 수 있다는 장점이 있지만, 관련된 컨텐츠의 위치(rank)를 점수에 반영할 수 없다는 문제점이 있다.(지난 글에서 언급했다시피 정밀도는 우선순위를 고려하는 기준이 아니므로)
그렇기 때문에 Precision@N처럼 상위 N개의 관련된 컨텐츠에 대해 전부 점수를 반영할 수 있되, 관련된 컨텐츠의 위치에 따라 점수에 차등을 줄 수 있는 평가 모델이 필요하다. MAP(Mean Average Precision)은 이러한 문제점을 해결할 수 있는 평가모델로써, 아래의 알고리즘을 이용하여 구할 수 있다.

위 알고리즘을 해석하면 아래와 같다.
- 각 사용자마다 관련된 컨텐츠를 구하여 해당 관련 컨텐츠 위치까지의 목록(sublist)에 대하여 정밀도를 계산한다.
- 계산된 정밀도 값들에 대하여 사용자별로 평균을 내고, 그 결과를 모두 모아 평균을 계산한다.
실제 예를 통해 이해하기 위해 아래 그림을 살펴보자.
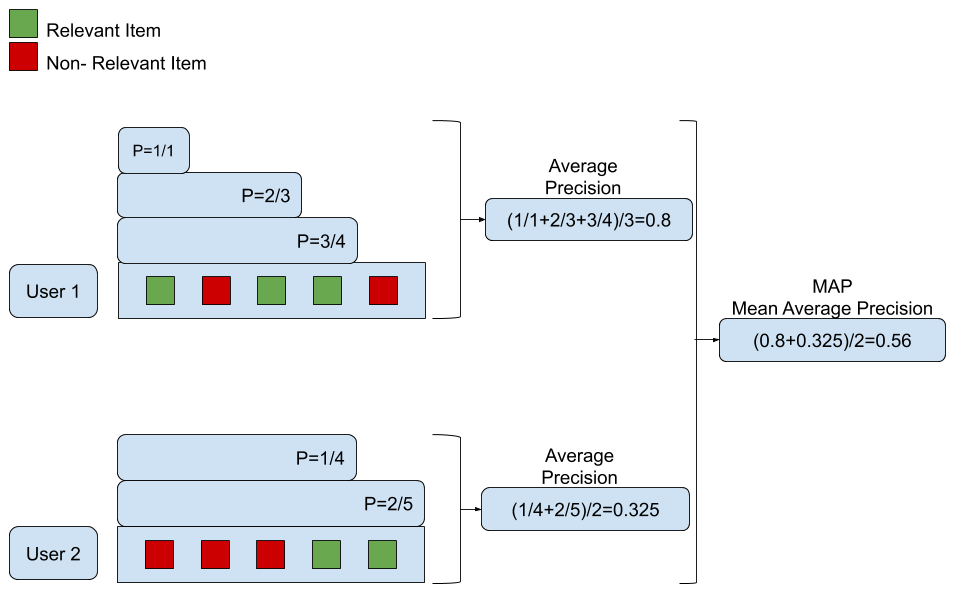
이 예에서는 사용자 2명에게 각각 5개의 추천 컨텐츠를 평가 대상으로 삼는다. 사용자 1의 경우 1,3,4번째 컨텐츠가 관련 컨텐츠이고, 사용자 2의 경우 4,5번째 컨텐츠가 관련 컨텐츠인 것을 확인할 수 있다. 사용자 1에 대해 평균 정밀도(average precision)을 계산하면 첫 번째 관련 컨텐츠까지 정밀도가 1/1 = 1이고, 다음 관련 컨텐츠인 세 번째 관련 컨텐츠까지 정밀도는 2/3(총 3개 중 2개가 관련된 컨텐츠)이다. 동일한 방법으로 네 번째 컨텐츠까지의 정밀도는 3/4이다. 이 3개의 정밀도 값 평균을 내면 사용자 1의 평균 정밀도인 (1/1+2/3+3/4)/3 = 0.8이 된다. 동일한 방법으로 사용자 2에 대한 평균 정밀도를 구하면 (1/4+2/5)/2 = 0.325가 된다. 이렇게 구해진 각 사용자의 평균 정밀도에 대하여 평균을 구하면 (0.8 + 0.325)/2 = 0.56이 되고 이 값이 해당 IR의 MAP 점수가 된다.
MAP 장점
- 추천 컨텐츠의 단순한 성능을 평가하는 것이 아니라 우선순위를 고려한 성능을 평가할 수 있다.
- 상위에 있는 오류(관련없는 컨텐츠)에 대해서는 가중치를 더 주고, 하위에 있는 오류에 대해서는 가중치를 적게 주어 관련 컨텐츠가 상위에 오를 수 있도록 도움을 준다.
MAP 단점
- MAP는 관련 여부가 명확하지 않은 경우에는 계산하기 어렵다.
- 1~5점으로 평가하는 평점같이 관련 여부를 판단하기 어려운 경우는 MAP를 사용하기 어렵다.(4~5점은 관련있다고 판단하더라도 3점은 관련 여부를 판단하기 어려울 것이다.)
이와 같이 MAP는 MRR과는 다르게 상위 N개의 추천 컨텐츠에 대하여 평가를 할 수 있고, precision@N과는 다르게 추천 컨텐츠의 우선순위를 고려하여 점수를 계산할 수 있다.
MAP은 전반적으로 훌륭한 평가 모델이 될 수 있다. 만약 컨텐츠의 관련 여부를 이분법으로 나눌 수 있다면 MAP은 좋은 평가 모델이 될 것이다. 하지만, 사용자에게 더 관련이 있는 컨텐츠를 상위에 노출시키고 있는지에 대해 평가하고 싶다면 다음에 설명하는 NDCG라는 평가 모델을 활용해야 한다.
NDCG
사실 NDCG(Normalized Discounted Cumulative Gain)는 MAP을 이용하여 얻고자하는 목표는 크게 다르지 않다. 다만 NDCG는 관련 여부에 대해 이분법적으로 구분하는 것이 아니라 더 관련있는 컨텐츠는 무엇인가?에 대해 집중하여 더 관련있는 컨텐츠를 덜 관련있는 컨텐츠보다 더 상위에 노출시키는지에 대해 평가한다. NDCG의 도출과정은 아래와 같다.
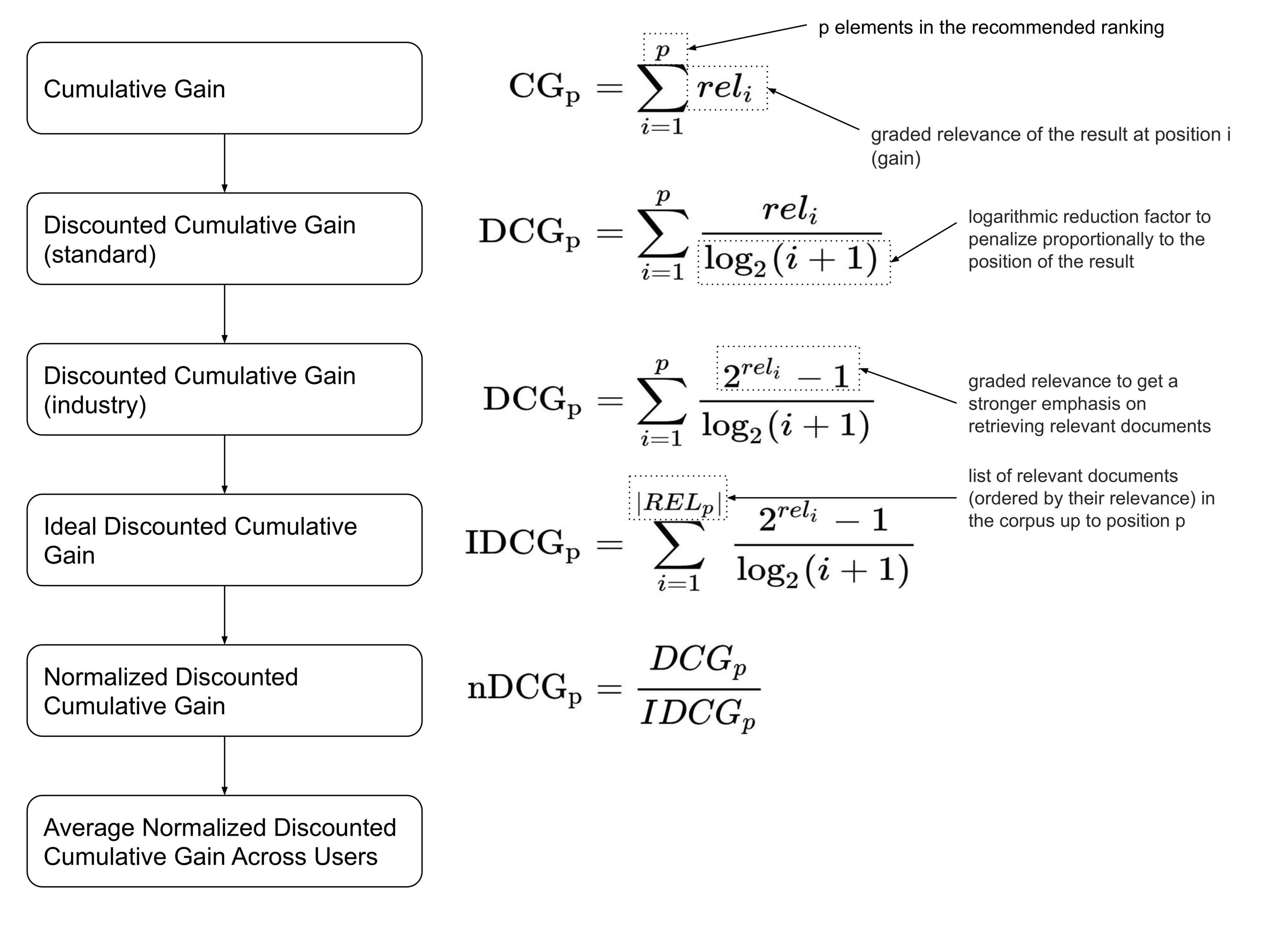
- 모든 추천 컨텐츠들의 관련도를 합하여 CG(cumulative gain)을 구한다.
- CG에서 추천 컨텐츠들의 관련도를 합하였다면, DCG는 각 추천 컨텐츠의 관련도를 log함수로 나누어 값을 구한다. log함수 특성상 위치 값이 클수록(하위에 있을 수록) DCG의 값을 더 작아지게 함으로써 상위 컨텐츠의 값을 점수에 더 반영할 수 있게 한다.
- DCG 값에 관련도를 더 강조하고 싶다면, 2^관련도 - 1과 같이 관련도의 영향을 증가시킬 수 있다.
- 사용자마다 제공되는 추천 컨텐츠의 DCG와는 별개로 IDCG(이상적인 DCG)를 미리 계산해놓는다.
- 각 사용자의 DCG를 IDCG로 나누어서 사용자별 NDCG를 구한다.
- 사용자별 NDCG의 평균을 구하여 해당 IR의 NDCG를 구한다.
실제 예를 통해 이해하기 위해 아래 그림을 살펴보자.
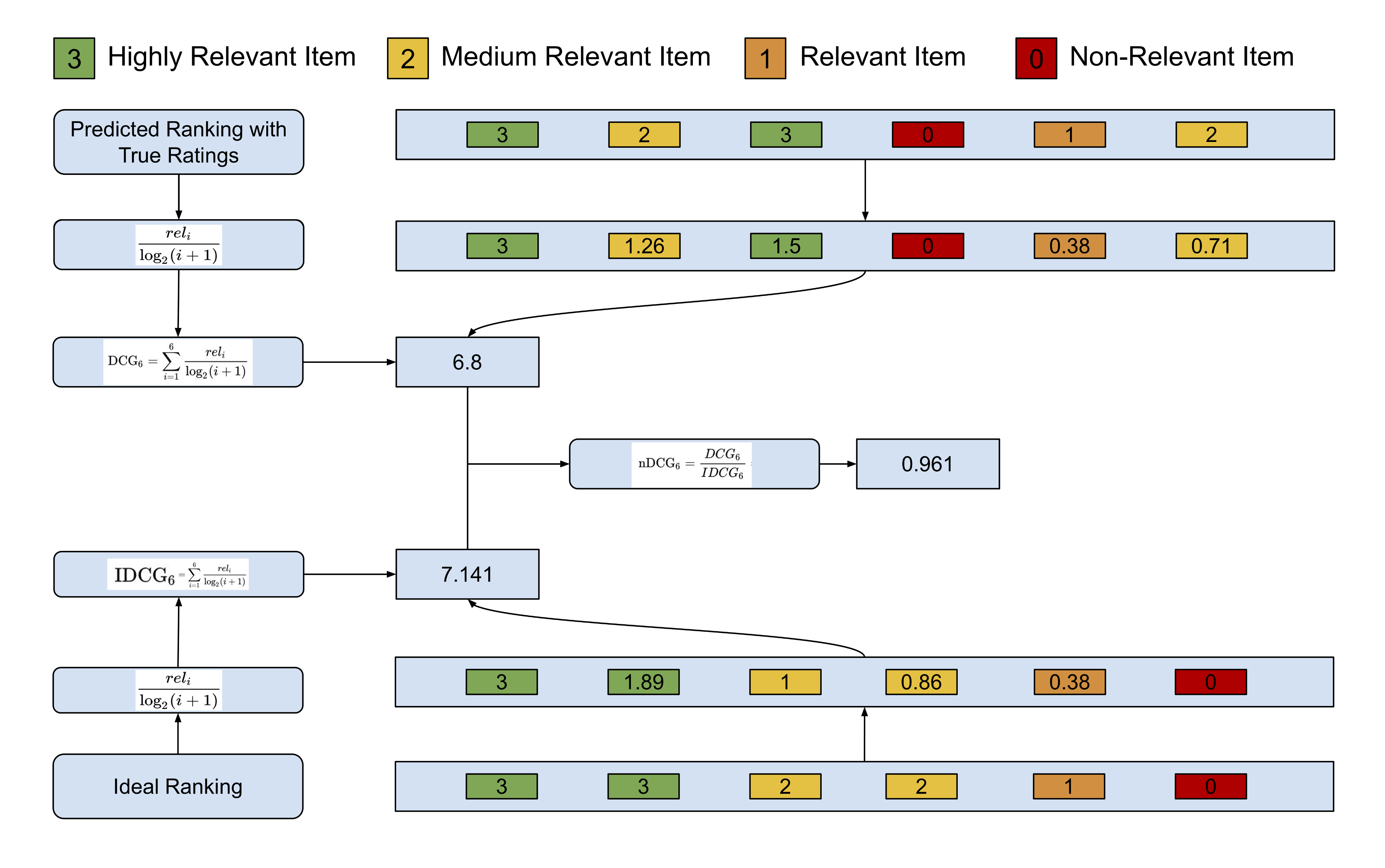
이 예는 기존 예와는 다르게 컨텐츠의 관련도를 이분법적으로 나누지 않고 0~3까지의 평점으로 관련도를 등급화하였다.
전체적으로 보면 추천 컨텐츠의 DCG와 해당 IR이 이상적으로 생각하는 IDCG를 구한 후, DCG를 IDCG로 나누어 사용자의 NDCG를 구한다. 그림 하단을 보면 IDCG를 구하는 과정을 볼 수 있는데, 총 6개의 추천 컨텐츠 중 1,2번째 컨텐츠는 3점을 받을 것으로 기대하고 있고, 3,4번째 컨텐츠는 2점, 5,6번째 컨텐츠는 각각 1점과 0점을 받을 것을 기대하고 있다. 이 기대치를 토대로 DCG를 구하면 3/log2*2 + 3/log2*3 + 2/log2*4 + 2/log2*5 + 1/log2*6 + 0/log2*7 = 7.141이 된다. 반면, 사용자의 추천 컨텐츠가 3,2,3,0,1,2 만큼 관련이 있다면, 계산법에 따라 3/log2*2 + 2/log2*3 + 3/log2*4 + 0/log2*5 + 1/log2*6 + 2/log2*7 = 6.8의 DCG를 구할 수 있다. 이렇게 구해진 DCG와 IDCG를 이용하여 6.8/7.141 = 0.961의 NDCG 값을 구할 수 있다. 이 NDCG는 사용자 한 명에 대한 NDCG이므로 IR의 NDCG를 구하고 싶다면, 각 사용자별 NDCG를 구하여 평균을 구하면 된다.
NDCG 장점
- 기존 방법과는 다르게 다양한 관련도에 대한 평가가 가능하다.
- 이분법적인 관련도에도 뛰어난 성능을 보인다.
- log 함수를 이용하여 하위 컨텐츠에 대한 영향을 줄임으로써 좋은 성능을 보인다.
NDCG 단점
- 사용자와의 관련성을 파악하기 어려운 상황에는 문제의 소지가 있다. 사용자가 컨텐츠에 대한 평가를 하지 않는다면(평점을 입력하지 않는 경우) 해당 관련도를 어떻게 처리해야 할지에 대해 정의해야 한다. 0점 처리해도 문제가 될 것이고, 평균 값을 이용해도 문제가 될 수 있다.
- 사용자의 관련 컨텐츠가 없다고 판단될 경우, 임의로 NDCG를 0으로 설정해주어야 한다.
- 보통 K개의 NDCG를 가지고 IR을 평가하는데 IR에서 제공한 컨텐츠가 K보다 부족한 경우, 부족한 관련도를 최소 점수로 채워서 계산해야 한다.
보다시피 NDCG는 특별한 경우가 아니고서는 훌륭한 평가 기준이 될 수 있다. 다만, 특별한 경우에 대해서 예외처리를 해주어야 하고 관련도에 대한 기준을 상황마다 명확하게 세워야 한다. 이런 부분을 감안하더라도 평점 기반의 추천 서비스에서 NDCG를 활용하면 좋은 평가를 할 수 있는 것이라 생각된다.
예제 코드
MRR, MAP, NDCG에 대한 샘플 코드는 샘플 코드에 개발해두었다.
마치며
지난 글부터 이번 글까지 IR을 평가할 수 있는 다양한 평가 모델에 대해서 설명했다.
- 만약 당신이 우선순위(rank)가 없는 IR을 사용한다면 정밀도와 재현율을 같이 사용해보도록 하자. IR에서 선정해준 컨텐츠가 얼마나 관련이 있는지, 관련성 있는 컨텐츠를 놓치지 않고 있는지 평가해줄 것이다.
- 만약 당신이 추천 시스템과 같이 우선순위가 중요한 IR을 사용한다면 MRR, MAP, NDCG를 고려해보자.
- 사용자가 잘 알만한 컨텐츠를 추천하고 추천하는 첫 번째 관련 컨텐츠가 중요하다면 MRR을 사용해보자.
- 추천 컨텐츠의 관련도를 이분법으로 판단할 수 있고, 추천 컨텐츠의 노출 위치가 중요하다면 MAP을 사용해보자.
- 추천 컨텐츠의 관련도를 여러 가지 값으로 표현할 수 있고, 관련도에 따른 가중치 조정을 하고 싶다면 NDCG을 사용해보자.
